
Las escaleras helicoidales permiten ahorrar metros cuadrados valiosos en ambientes pequeños y conectar los diferentes niveles de un edificio ocupando un área mucho menor que una escalera convencional. Pueden también ser objetos icónicos en los proyectos, con formas atrevidas y configuraciones diversas. Sin embargo, su diseño requiere atención, para evitar que se vuelvan incómodas o peligrosas. Aunque actualmente los softwares BIM están simplificando este proceso, siempre es importante entender las restricciones y algunos de los conceptos básicos para un diseño adecuado.
Las escaleras helicoidales pueden adoptar diferentes configuraciones estructurales. Las más comunes tienen un formato circular y cuentan con un mástil central desde donde se fijan los peldaños.

Para su diseño, se deb tomar en cuenta tres factores principales:
- ¿Cuánto debe salvar la escalera verticalmente? (Distancia entre pisos);
- ¿Cuál es su ángulo de rotación?;
- ¿Cuál es su diámetro?
Es importante tener claro dónde comenzará y donde terminará la escalera en el nivel superior, de acuerdo a los flujos pensados en planta. Esto significa: calcular su ángulo de rotación. Si es necesario, existen algunas aplicaciones gratuitas que ayudan en el proceso. Para medir el número de escalones, es imprescindible conocer su longitud total, que en una circunferencia se refiere al perímetro. Deberás –entonces– recordar las clases de matemáticas y aplicar algunas fórmulas. Para calcular el perímetro total, utiliza la siguiente fórmula:
Perímetro (longitud de la escalera helicoidal) = (π (Pi) x radio x ángulo de rotación) / 180)

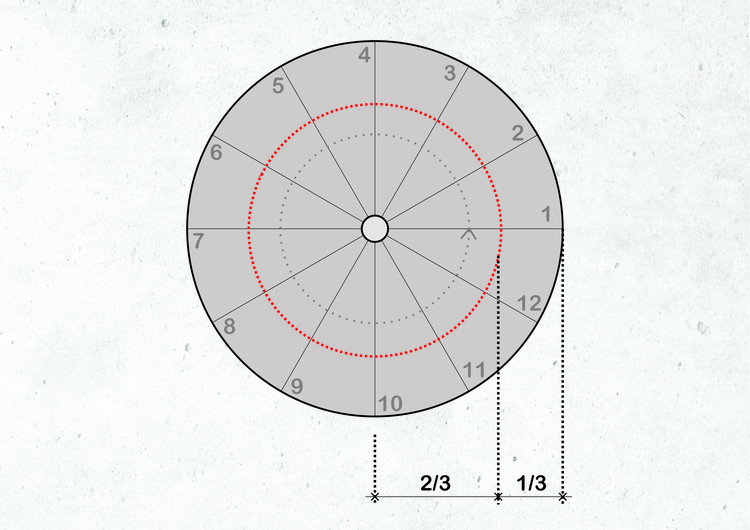

Sin embargo, considerando que los escalones cuentan con formas irregulares (aproximándose al mástil central) es importante definir una porción sobre la cual realizar el cálculo de los pisos de la escalera. Se considera que esta "línea útil", por donde el usuario camina, se encuentra ubicada a 2/3 del centro del radio.
Habiendo determinado esta porción, se puede adoptar el mismo método de una escalera convencional, como les indicamos en este artículo. La única diferencia es que, al existir una mayor dificultad para adaptarse a la fórmula de blondel, se debe utilizar una tolerancia un poco más alta.
Por ejemplo, se tiene una distancia de 3.00 m entre losas y el espacio para una escalera de 100 cm de radio. De acuerdo con su disposición en el espacio, la escalera comenzará en el mismo punto donde acabará, o sea, tendrá un ángulo de rotación de 360°. Al insertar los valores en la fórmula anterior, su perímetro total será de 6,28 m.
Para encontrar la línea útil, se calculan los 2/3 del valor del perímetro de la circunferencia, llegando a una longitud útil de 4.18 metros, donde las personas pisarán. Si intentamos 15 escalones, tendremos huellas de 27 cm y contrahuellas de 20 cm. Aplicando la ley de blondel, acabamos con un total de 67, lo que se excedería levemente de una escalera convencional. En una escalera helicoidal, con ciertas restricciones, ese valor puede ser aceptado.

Aunque el radio mínimo a ser considerado en una escalera helicoidal es de 70 centímetros, siempre debes darle preferencia a las escaleras con al menos 80 centímetros de radio. Se debe tener en cuenta, además, una altura mínima de 2.15 metros entre los escalones y el techo, o los escalones superiores.
Siguiendo estas recomendaciones podrás tener mayor autonomía al proponer una escalera helicoidal. ¡No tengas miedo, suelta tu creatividad y diseña una escalera interesante y funcional!


